如图，已知二次函数L1：y=x2﹣4x+3与x轴交于A．B两点（点A在点B左边），与y轴交于点C．
（1）写出二次函数L1的开口方向、对称轴和顶点坐标；
（2）研究二次函数L2：y=kx2﹣4kx+3k（k≠0）．
①写出二次函数L2与二次函数L1有关图象的两条相同的性质；
②若直线y=8k与抛物线L2交于E、F两点，问线段EF的长度是否发生变化？如果不会，请求出EF的长度；如果会，请说明理由．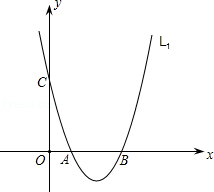
相关试题
小明从今年1月初起刻苦练习跳远，每个月的跳远成绩都比上一个月有所增加，而且增加的距离相同．2月份，5月份他的跳远成绩分别为4．1m，4．7m．请你算出小明1月份的跳远成绩以及每个月增加的距离．
，并把它的解集在数轴上表示出来．
相关知识点
推荐套卷
粤公网安备 44130202000953号