某培训班共有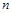 名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在
名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在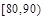 内的频数为36.
内的频数为36.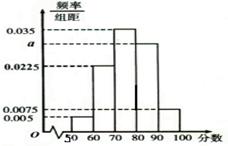
(1)请根据图中所给数据,求出a及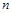 的值;
的值;
(2)从如图5组中按分层抽样的方法选取40名学生的成绩作为一个样本,求在第一组、第五组(从左到右)中分别抽取了几名学生的成绩?
(3)在(2)抽取的样本中的第一与第五组中,随机抽取两名学生的成绩,求所取两名学生的平均分不低于70分的概率.
相关知识点
推荐套卷
某培训班共有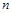 名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在
名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在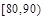 内的频数为36.
内的频数为36.
(1)请根据图中所给数据,求出a及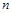 的值;
的值;
(2)从如图5组中按分层抽样的方法选取40名学生的成绩作为一个样本,求在第一组、第五组(从左到右)中分别抽取了几名学生的成绩?
(3)在(2)抽取的样本中的第一与第五组中,随机抽取两名学生的成绩,求所取两名学生的平均分不低于70分的概率.