如图所示,制作一种产品,需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为l5℃,加热5分钟使材料温度达到60℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时问x成反比例函数关系.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系(要写出x的取值范);
(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间为多少分钟?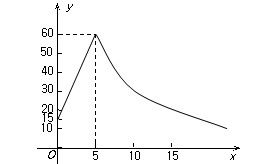
相关知识点
推荐套卷
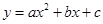 与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在 轴上且AD为⊙M的直径.点E是⊙M与
轴上且AD为⊙M的直径.点E是⊙M与 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧 上的点F作FH⊥AD于点H,且FH=1.5.
上的点F作FH⊥AD于点H,且FH=1.5.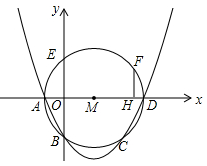
 .
.
 的值.
的值. ,且根据我市的地理位置设定太阳能板AB的倾斜角为
,且根据我市的地理位置设定太阳能板AB的倾斜角为 ,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍旋转,叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得
,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍旋转,叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得 ,
, ,
, ,结果保留两位小数)
,结果保留两位小数)

 的度数是____________;
的度数是____________; 粤公网安备 44130202000953号
粤公网安备 44130202000953号