如图,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①② ③;①③
③;①③ ②;②③
②;②③ ①.
①.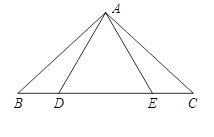
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
相关知识点
推荐套卷
如图,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①② ③;①③
③;①③ ②;②③
②;②③ ①.
①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).