如图已知二次函数图象的顶点为原点, 直线 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.
(1)求这个二次函数的解析式与B点坐标;
(2) 为线段
为线段 上的一个动点(点
上的一个动点(点 与
与 不重合),过
不重合),过 作
作 轴的垂线与这个二次函数的图象交于D点,与
轴的垂线与这个二次函数的图象交于D点,与 轴交于点E.设线段PD的长为
轴交于点E.设线段PD的长为 ,点
,点 的横坐标为t,求
的横坐标为t,求 与t之间的函数关系式,并写出自变量t的取值范围;
与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段 上是否存在点
上是否存在点 ,使得以点P、D、B为顶点的三角形与
,使得以点P、D、B为顶点的三角形与 相似?若存在,请求出
相似?若存在,请求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

相关知识点
推荐套卷
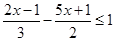 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.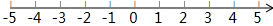
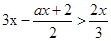 的解,求a的取值范围.
的解,求a的取值范围.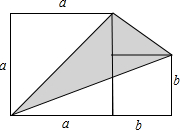

 粤公网安备 44130202000953号
粤公网安备 44130202000953号