如图，已知射线DM与直线BC交于点A，AB∥DE.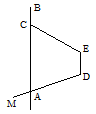
（1）若当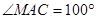
，
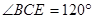时，问把EC绕点E再旋转多大角度时，可判定MD∥EC，请你设计出两种方案，并画出草图（旋转后若EC与AB相交，则交点用
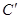表示）.
（2）若将EC绕点E逆时针旋转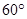
时，点C与点A恰好重合，请画出草图，并在图中找出同位角、内错角各两对（先用数字标出角，再回答）.
相关试题
如图，已知射线DM与直线BC交于点A，AB∥DE.
（1）若当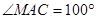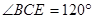，时，问把EC绕点E再旋转多大角度时，可判定MD∥EC，请你设计出两种方案，并画出草图（旋转后若EC与AB相交，则交点用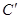表示）.
（2）若将EC绕点E逆时针旋转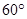时，点C与点A恰好重合，请画出草图，并在图中找出同位角、内错角各两对（先用数字标出角，再回答）.
，且点A、B到原点的距离相等，求x的值．
，求（2@6）@8的值．
粤公网安备 44130202000953号