在平面直角坐标系中，抛物线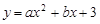
与
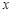轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）直接填写：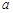
= ，b= ，顶点C的坐标为 ；
（2）在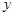
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标. 
相关试题
如图是某城市出租车单程收费Y（元）与行驶路程X（千米）之间的函数关系图像，根据图像回答下列问题：
（1）从图像上你能得到哪些信息？（请写出2条）
（2）求出收费Y（元）与行驶路程X（千米）（X≥3）之间的函数关系式。
●
●
的图像经过点（－2，4）且与直线
平行，求这个一次函数的解析式。
相关知识点
推荐套卷
粤公网安备 44130202000953号