如图，在平面直角坐标系中，矩形OABC的顶点A(0，3)、C(－1，0)．将矩形OABC绕原点O顺时针方向旋转90o，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线经过点C、M、N．解答下列问题：
(1)求直线BB′的 函数解析式；
(2)求抛物线的解析式；
(3)在抛物线上求出使S△PB′′ C′=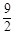
S矩形OABC的所有点P的坐标． 
；
，且
异号，
是绝对值最小的负整数，
，求3A·B-
A·C的值.
，其中
.相关知识点
推荐套卷
如图，在平面直角坐标系中，矩形OABC的顶点A(0，3)、C(－1，0)．将矩形OABC绕原点O顺时针方向旋转90o，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线经过点C、M、N．解答下列问题：
(1)求直线BB′的 函数解析式；
(2)求抛物线的解析式；
(3)在抛物线上求出使S△PB′′ C′=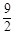S矩形OABC的所有点P的坐标．
粤公网安备 44130202000953号