已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（11，0），点B（0，6），点P为BC边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP=t．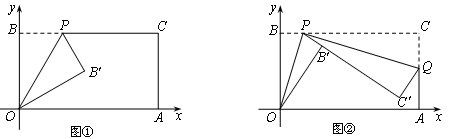
（Ⅰ）如图①，当∠BOP=300时，求点P的坐标；
（Ⅱ）如图②，经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，若AQ=m，试用含有t的式子表示m；
（Ⅲ）在（Ⅱ）的条件下，当点C′恰好落在边OA上时，求点P的坐标（直接写出结果即可）．
湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了 淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本 放养总费用 收购成本）．
（1）设每天的放养费用是 万元，收购成本为 万元，求 和 的值；
（2）设这批淡水鱼放养 天后的质量为 ，销售单价为 元 ．根据以往经验可知： 与 的函数关系为 ； 与 的函数关系如图所示．
①分别求出当 和 时， 与 的函数关系式；
②设将这批淡水鱼放养 天后一次性出售所得利润为 元，求当 为何值时， 最大？并求出最大值．（利润 销售总额 总成本）
已知正方形 的对角线 ， 相交于点 ．
（1）如图1， ， 分别是 ， 上的点， 与 的延长线相交于点 ．若 ，求证： ；
（2）如图2， 是 上的点，过点 作 ，交线段 于点 ，连接 交 于点 ，交 于点 ．若 ，
①求证： ；
②当 时，求 的长．
为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了20天的调查，将所得数据绘制成如下统计图（图2不完整）
请根据所给信息，解答下列问题：
（1）第7天，这一路口的行人交通违章次数是多少次？这20天中，行人交通违章6次的有多少天？
（2）请把图2中的频数直方图补充完整；（温馨提示：请画在答题卷相对应的图上）
（3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了4次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？
粤公网安备 44130202000953号