有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式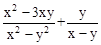 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简分式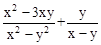 ,并求使分式的值为整数的(x,y)出现的概率.
,并求使分式的值为整数的(x,y)出现的概率.
推荐套卷
有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式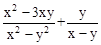 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简分式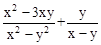 ,并求使分式的值为整数的(x,y)出现的概率.
,并求使分式的值为整数的(x,y)出现的概率.