某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系式如图所示．
（1）求y关于x的函数解析式，并写出它的定义域；
（2）当生产这种产品的总成本为280万元时，求该产品的生产数量．
（注：总成本=每吨的成本×生产数量）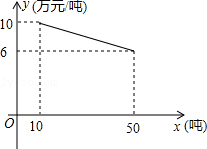
相关试题
的
点平移到
，
，
的坐标
∥
．直线
与直线
、点
，
，垂足为点
，若
，求
的度数．
中，
是
边上的高，
是
平分线.
，
。
的度数；
的度数．
相关知识点
推荐套卷
某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系式如图所示．
（1）求y关于x的函数解析式，并写出它的定义域；
（2）当生产这种产品的总成本为280万元时，求该产品的生产数量．
（注：总成本=每吨的成本×生产数量）
粤公网安备 44130202000953号