如图,某旅游区拟在公路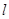 (南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路
(南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路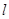 的距离与到
的距离与到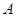 处的距离相等,并在湖中建造一个三角形的游乐区
处的距离相等,并在湖中建造一个三角形的游乐区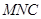 ,三个顶点
,三个顶点 都在湖沿岸上,直线通道
都在湖沿岸上,直线通道 经过
经过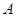 处.经测算,
处.经测算,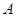 在公路
在公路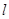 正东方向
正东方向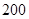 米处,
米处,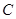 在
在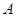 的正西方向
的正西方向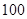 米处,现以点
米处,现以点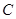 为坐标原点,以线段
为坐标原点,以线段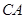 所在直线为
所在直线为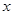 轴建立平面直角坐标系,
轴建立平面直角坐标系,
(1)求抛物线的方程
(2)试确定直线通道 的位置,使得三角形游乐区
的位置,使得三角形游乐区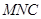 的面积最小,并求出最小值
的面积最小,并求出最小值
相关知识点
推荐套卷
如图,某旅游区拟在公路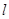 (南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路
(南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路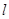 的距离与到
的距离与到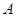 处的距离相等,并在湖中建造一个三角形的游乐区
处的距离相等,并在湖中建造一个三角形的游乐区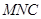 ,三个顶点
,三个顶点 都在湖沿岸上,直线通道
都在湖沿岸上,直线通道 经过
经过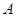 处.经测算,
处.经测算,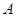 在公路
在公路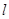 正东方向
正东方向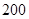 米处,
米处,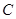 在
在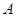 的正西方向
的正西方向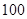 米处,现以点
米处,现以点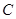 为坐标原点,以线段
为坐标原点,以线段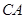 所在直线为
所在直线为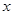 轴建立平面直角坐标系,
轴建立平面直角坐标系,
(1)求抛物线的方程
(2)试确定直线通道 的位置,使得三角形游乐区
的位置,使得三角形游乐区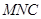 的面积最小,并求出最小值
的面积最小,并求出最小值