如图,已知线段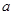 .
.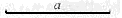
(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=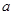 ,BC=
,BC=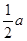 (要求保留作图痕迹,不必写出作法);
(要求保留作图痕迹,不必写出作法);
(2)若在(1)作出的RtΔABC中,AB=4cm,求AC边上的高 .
相关知识点
推荐套卷
如图,已知线段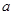 .
.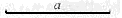
(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=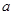 ,BC=
,BC=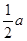 (要求保留作图痕迹,不必写出作法);
(要求保留作图痕迹,不必写出作法);
(2)若在(1)作出的RtΔABC中,AB=4cm,求AC边上的高 .