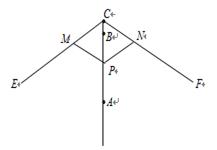
图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点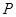 与点
与点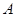 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点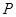 由
由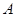 向
向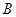 移动;当点
移动;当点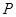 到过点
到过点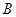 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有 分米,
分米,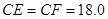 分米,
分米, 分米
分米
(1)求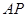 长的取值范围; (2)当
长的取值范围; (2)当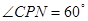 时,求
时,求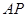 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为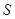 (结果保留
(结果保留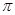 ).
).
相关知识点
推荐套卷
图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点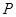 与点
与点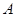 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点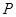 由
由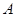 向
向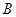 移动;当点
移动;当点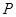 到过点
到过点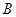 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有 分米,
分米,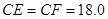 分米,
分米, 分米
分米
(1)求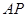 长的取值范围; (2)当
长的取值范围; (2)当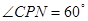 时,求
时,求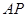 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为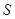 (结果保留
(结果保留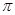 ).
).
