如图,在等腰梯形ABCD中,AD∥BC,点M,N分别是AD,BC的中点,点E,F分别是BM,CM的中点.
(1)求证:四边形MENF是菱形;
(2)当四边形MENF是正方形时,求证:等腰梯形ABCD的高是底边BC的一半.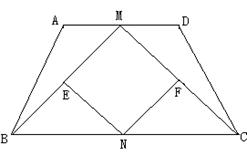
相关知识点
推荐套卷
如图,在等腰梯形ABCD中,AD∥BC,点M,N分别是AD,BC的中点,点E,F分别是BM,CM的中点.
(1)求证:四边形MENF是菱形;
(2)当四边形MENF是正方形时,求证:等腰梯形ABCD的高是底边BC的一半.