某商场计划采购甲、乙、丙三种型号的“格力”牌空调共25台．三种型号的空调进价和售价如下表：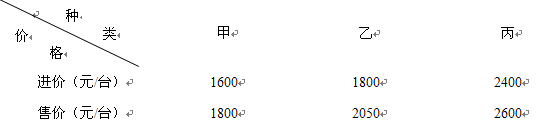
商场计划投入总资金5万元，所购进的甲、丙型号空调数量相同，乙型号数量不超过甲型号数量的一半．若设购买甲型号空调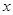
台，所有型号空调全部售出后获得的总利润为
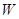元．
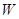（1）求与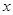之间的函数关系式．
（2）商场如何采购空调才能获得最大利润？
（3）由于原材料上涨，商场决定将丙型号空调的售价提高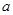
元（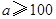
），其余型号售价不变，则商场又该如何采购才能获得最大利润？
相关试题
如图，将□ABCD沿过点A的直线
折叠，使点D落到AB边上的点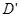
处，折痕交CD边于点E，连接BE
（1）求证：四边形
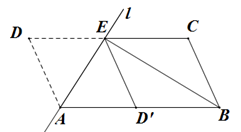
是平行四边形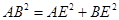
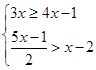（2）若BE平分∠ABC，求证：
(本题满分8分）在“爱满扬州”慈善一日捐活动中，学校团总支为了了解本校学生的捐款情况，随机抽取了50名学生的捐款数进行了统计，并绘制成下面的统计图。
（1）这50名同学捐款的众数为元，中位数为元
（2）求这50名同学捐款的平均数
（3）该校共有600名学生参与捐款，请估计该校学生的捐款总数
，并把它的解集在数轴上表示出来
的图象交x轴于A（﹣1，0）、B（3，0）两点，交y轴于点C，连接BC，动点P以每秒1个单位长度的速度从A向B运动，动点Q以每秒
个单位长度的速度从B向C运动，P、Q同时出发，连接PQ，当点Q到达C点时，P、Q同时停止运动，设运动时间为t秒．
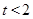时，延长QP交y轴于点M，在抛物线上是否存在一点N，使得PQ的中点恰为MN的中点？若存在，求出点N的坐标与t的值；若不存在，请说明理由．相关知识点
推荐套卷
粤公网安备 44130202000953号