(本小题满分10分)已知二次函数f (x) = x2 – 16x + p + 3.
(1)若函数在区间 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时, 的值域为区间
的值域为区间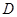 ,且
,且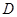 的长度为
的长度为
12 – q.(注:区间[a,b](a<b)的长度为b – a)
推荐套卷
(本小题满分10分)已知二次函数f (x) = x2 – 16x + p + 3.
(1)若函数在区间 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时, 的值域为区间
的值域为区间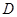 ,且
,且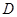 的长度为
的长度为
12 – q.(注:区间[a,b](a<b)的长度为b – a)