设
是单位圆
上的任意一点,
是过点
与
轴垂直的直线,
是直线
与
 轴的交点,点
在直线
上,且满足
. 当点
在圆上运动时,记点
的轨迹为曲线
.
(Ⅰ)求曲线
的方程,判断曲线
为何种圆锥曲线,并求其焦点坐标;
(Ⅱ)过原点且斜率为
的直线交曲线
于
,
两点,其中
在第一象限,它在
轴上的射影为点
,直线
交曲线
于另一点
. 是否存在
,使得对任意的
,都有
?若存在,求
的值;若不存在,请说明理由.
推荐套卷
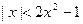 .
. 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱
,三棱柱的底面为圆柱 是圆
是圆 的直径。
的直径。 平面
平面 ;
; ,在圆
,在圆 柱
柱 。
。 在圆周上运动时,求
在圆周上运动时,求 与平面
与平面 所成的角为
所成的角为 。当
。当
 的值。
的值。 B=2,BC=
B=2,BC= 的矩形,侧面PAB
的矩形,侧面PAB
 粤公网安备 44130202000953号
粤公网安备 44130202000953号