(12分)用简单随机抽样从含有8个个体的总体中抽取一个容量为2的样本.问:
①总体中的某一个体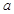 在第一次抽取时被抽到的概率是多少?
在第一次抽取时被抽到的概率是多少?
②个体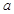 在第1次未被抽到,而第2次被抽到的概率是多少?
在第1次未被抽到,而第2次被抽到的概率是多少?
③在整个抽样过程中,个体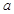 被抽到的概率是多少?
被抽到的概率是多少?
相关知识点
推荐套卷
(12分)用简单随机抽样从含有8个个体的总体中抽取一个容量为2的样本.问:
①总体中的某一个体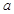 在第一次抽取时被抽到的概率是多少?
在第一次抽取时被抽到的概率是多少?
②个体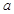 在第1次未被抽到,而第2次被抽到的概率是多少?
在第1次未被抽到,而第2次被抽到的概率是多少?
③在整个抽样过程中,个体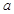 被抽到的概率是多少?
被抽到的概率是多少?