我县开展小组合作学习，为了解学生课堂发言情况，随机抽取某校九年级部分学生，对他们每天在课堂上发言的次数进行调查和统计，统计表如下，并绘制了两幅不完整的统计图．已经知A、B两组发言人数直方图高度比为1:5．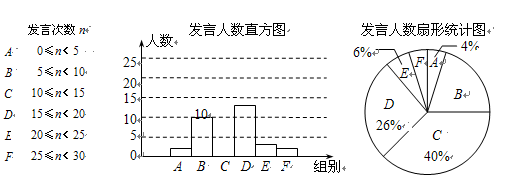
请结合图中相关的数据回答下列问题：
（1）A组的人数是多少？本次调查的样本容量是多少？
（2）求出C组的人数并补全直方图．
（3）该校九年级共有250人，请估计全年级每天在课堂上发言次数不少于15次的人数．
相关试题
李明家和陈刚家都从甲、乙两供水点购买同一种桶装矿泉水，李明家第一季度从甲、乙两供水点分别购买了10桶和6桶，共花费51元；陈刚家第一季度从甲、乙两供水点分别购买了8桶和12桶，且在乙供水点比在甲供水点多花18元钱.若只考虑价格因素，通过计算说明到哪家供水点购买在喝种桶装矿泉水更便宜一些？
的二元一次方程组
的解是
，那么关于
的解是什么？
相关知识点
推荐套卷
粤公网安备 44130202000953号