如图，在平面直角坐标系中：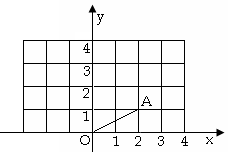
（1）写出点A的坐标；
（2）将线段OA向上平移两次，每次平移1个单位，再将线段向左平移2个单位，得到线段O′A′，写出点O、A的对应点O′、A′的坐标；
（3）在图中画出与线段OA相等的两条不同的线段．
相关试题
—
=8
，其中x＝－4．
(本小题满分12分)
如图，在平面直角坐标系
中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知
，
，△ABC的面积
，抛物线
经过A、B、C三点。
(1)求此抛物线的函数表达式；
(2)设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；
(3)在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为
？若存在，求出点M的坐标；若不存在，请说明理由．
，AD=
(相关知识点
推荐套卷
粤公网安备 44130202000953号