小红用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面点E处放一面平面镜，镜子与教学大楼的距离
米。当她与镜子的距离
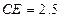米时，她刚好能从镜子中看到教学大楼的顶端B。已知她的眼睛距地面高度
米，请你帮助小红测量出大楼AB的高度（注：入射角＝反射角）
中，
，
，点O在
，求：
的度数.
中, 
，CD平分
交AB于D点，若
.求：
的度数.
中，D是AC上一点，且
，
.求：
的度数.
中，
，
，
，求
的度数.
相关知识点
推荐套卷
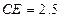小红用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面点E处放一面平面镜，镜子与教学大楼的距离米。当她与镜子的距离米时，她刚好能从镜子中看到教学大楼的顶端B。已知她的眼睛距地面高度米，请你帮助小红测量出大楼AB的高度（注：入射角＝反射角）
粤公网安备 44130202000953号