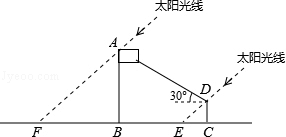
(年贵州六盘水14分)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据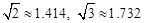 ,)
,)
(年贵州六盘水14分)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据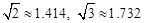 ,)
,)