荆门市是著名的“鱼米之乡”.某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼(俗称黑鱼)共75千克,且乌鱼的进货量大于40千克.已知草鱼的批发单价为8元/千克,乌鱼的批发单价与进货量的函数关系如图所示.
(1)请直接写出批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式;
(2)若经销商将购进的这批鱼当日零售,草鱼和乌鱼分别可卖出89%、95%,要使总零售量不低于进货量的93%,问该经销商应怎样安排进货,才能使进货费用最低?最低费用是多少?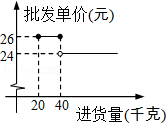
相关知识点
推荐套卷
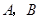 两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套
两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套 型桌椅(一桌两椅)需木料
型桌椅(一桌两椅)需木料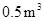 ,一套
,一套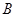 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料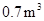 ,工厂现有库存木料
,工厂现有库存木料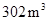 .
.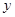 (元)与生产
(元)与生产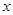 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用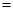 生产成本
生产成本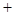 运费)
运费)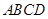 中,
中,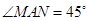 ,
,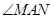 绕点
绕点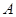 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交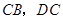 (或它们的延长线)于点
(或它们的延长线)于点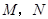 .
.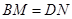 时(如图1),易证
时(如图1),易证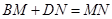 .
.
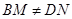 时(如图2),线段
时(如图2),线段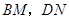 和
和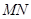 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.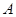 地逆流而上,前往
地逆流而上,前往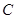 地营救受困群众,途经
地营救受困群众,途经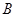 地时,由所携带的救生艇将
地时,由所携带的救生艇将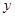 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间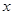 之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.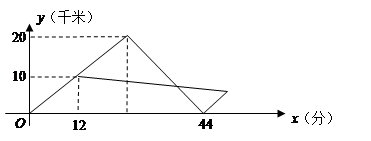
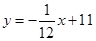 ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离 三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一: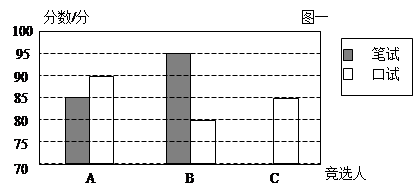

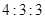 的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.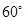 的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.
的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号