如图所示,有一条等宽(AF=EC)的小路穿过矩形的草地ABCD,已知AB="60m," BC="84m," AE=100m.
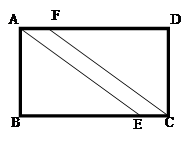
(1)试判断这条小路(四边形AECF)的形状,并说明理由;
(2)求这条小路的的面积和对角线FE的长度.(精确到整数)
相关知识点
推荐套卷
如图所示,有一条等宽(AF=EC)的小路穿过矩形的草地ABCD,已知AB="60m," BC="84m," AE=100m.

(1)试判断这条小路(四边形AECF)的形状,并说明理由;
(2)求这条小路的的面积和对角线FE的长度.(精确到整数)