知识背景：恩施来凤有一处野生古杨梅群落，其野生杨梅是一种具特殊价值的绿色食品．在当地市场出售时，基地要求“杨梅”用双层上盖的长方体纸箱封装（上盖纸板面积刚好等于底面面积的2倍，如图）
实际运用：如果要求纸箱的高为0.5米，底面是黄金矩形（宽与长的比是黄金比，取黄金比为0.6），体积为0.3立方米．
①按方案1（如图）做一个纸箱，需要矩形硬纸板
的面积是多少平方米？
②小明认为，如果从节省材料的角度考虑，采用方案2（如图）的菱形硬纸板
做一个纸箱比方案1更优，你认为呢？请说明理由．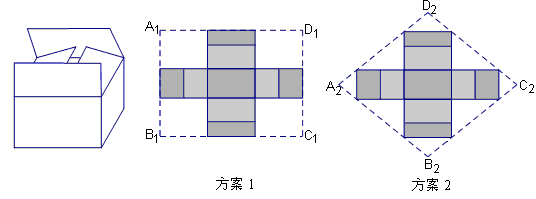
相关试题
某市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程．已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同，求甲、乙工程队每天各能铺设多少米？
小明去超市买三种商品，其中丙商品单价最贵，如果购买
件甲商品、
件乙商品和
件丙商品，那么需要付费
元，如果购
件甲商品、件乙商品和件丙商品，那么需要付费
元．
（1）如果购买三种商品各件，那么需要付费多少元？
（2）如果需要购买件甲商品、件乙商品和件丙商品，那么小明至少带多少钱才能保证一定能全部买到？（结果精算到元）
，
为原点
的面积
在坐标轴上，且三角形
的面积为
，求点
的不等式组
为何值时，该不等式组的解集为
个正整数解，求一个满足条件的整数
，垂足分别为
，且
相关知识点
推荐套卷
粤公网安备 44130202000953号