平面直角坐标系xOy中，抛物线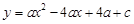
与x轴交于点A、点B，与y轴的正半轴交于点C，点 A的坐标为 (1, 0)，OB=OC，抛物线的顶点为D．
(1) 求此抛物线的解析式；
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB，求点P的坐标；
(3) Q为线段BD上一点，点A关于∠AQB的平分线的对称点为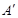
，若
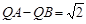，求点Q的坐标和此时△
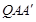的面积．
相关试题
，点A的坐标为(－3，1).(1)、求点B的坐标；(2)、求过A、O、B三点的抛物线的解析式；(3)、设点P为抛物线上到X轴的距离为1的点，点B关于抛物线的对称轴
的对称点为
， 求点P的坐标和
的面积．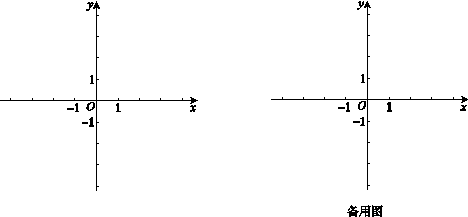 
相关知识点
推荐套卷
平面直角坐标系xOy中，抛物线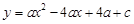与x轴交于点A、点B，与y轴的正半轴交于点C，点 A的坐标为 (1, 0)，OB=OC，抛物线的顶点为D．
(1) 求此抛物线的解析式；
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB，求点P的坐标；
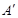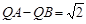(3) Q为线段BD上一点，点A关于∠AQB的平分线的对称点为，若，求点Q的坐标和此时△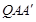的面积．
粤公网安备 44130202000953号