（本题10分）在直角坐标系xOy中，曲线C1的参数方程为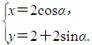
(α为参数)M是C1上的动点，P点满足
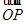＝2
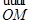，P点的轨迹为曲线C2.
(1)求C2的参数方程；
(2)在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ＝
与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|.
相关试题
推荐套卷
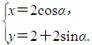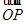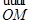（本题10分）在直角坐标系xOy中，曲线C1的参数方程为 (α为参数)M是C1上的动点，P点满足＝2，P点的轨迹为曲线C2.
(1)求C2的参数方程；
(2)在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ＝与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|.
粤公网安备 44130202000953号