(本小题满分13分)
在平面直角坐标系中,已知 ,若实数
,若实数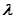 使得
使得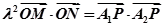 (
( 为坐标原点)
为坐标原点)
(1)求 点的轨迹方程,并讨论
点的轨迹方程,并讨论 点的轨迹类型;
点的轨迹类型;
(2)当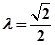 时,若过点
时,若过点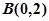 的直线与(1)中
的直线与(1)中 点的轨迹交于不同的两点
点的轨迹交于不同的两点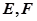 (
( 在
在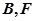 之间),试求
之间),试求 与
与 面积之比的取值范围。
面积之比的取值范围。
推荐套卷
(本小题满分13分)
在平面直角坐标系中,已知 ,若实数
,若实数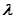 使得
使得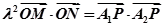 (
( 为坐标原点)
为坐标原点)
(1)求 点的轨迹方程,并讨论
点的轨迹方程,并讨论 点的轨迹类型;
点的轨迹类型;
(2)当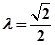 时,若过点
时,若过点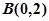 的直线与(1)中
的直线与(1)中 点的轨迹交于不同的两点
点的轨迹交于不同的两点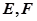 (
( 在
在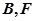 之间),试求
之间),试求 与
与 面积之比的取值范围。
面积之比的取值范围。