如图，矩形ABCD中，AB=4，AD=5，将矩形ABCD绕点A顺时针旋转，得到矩形AMNP，直线MN分别与边BC、CD交于点E、F.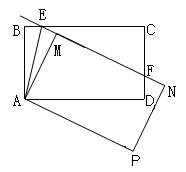
判断BE与ME的数量关系，并加以证明；
当△CEF是等腰三角形时，求线段BE的长；
设x=BE，y=CF·（AB2-BE2），试求y与x之间的函数关系式，并求出y的最大值.
相关知识点
推荐套卷
如图，矩形ABCD中，AB=4，AD=5，将矩形ABCD绕点A顺时针旋转，得到矩形AMNP，直线MN分别与边BC、CD交于点E、F.判断BE与ME的数量关系，并加以证明；
当△CEF是等腰三角形时，求线段BE的长；
设x=BE，y=CF·（AB2-BE2），试求y与x之间的函数关系式，并求出y的最大值.
粤公网安备 44130202000953号