平面图形
如图所示，其中
是矩形，
，
，
。现将该平面图形分别沿
和
折叠，使
与
所在平面都与平面
垂直，再分别连接
,得到如图2所示的空间图形，对此空间图形解答下列问题
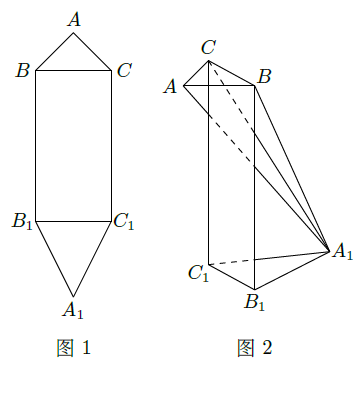
（Ⅰ）证明：
；
（Ⅱ）求
的长；
（Ⅲ）求二面角
的余弦值.
相关试题
+
+
+…+
的值的一个程序，要求写出算法，并用基本语句编写程序．
）．
的值．
满足
，且
，设
与
的夹角为θ．
（θ）＝
的最小值．
．
（x）的最小正周期和单调递增区间；
上的最大值和最小值．
＜α＜π，且
，
，求cos（α＋β）的值．推荐套卷
平面图形
如图所示，其中
是矩形，
，
，
。现将该平面图形分别沿
和
折叠，使
与
所在平面都与平面
垂直，再分别连接
,得到如图2所示的空间图形，对此空间图形解答下列问题
（Ⅰ）证明：
；
（Ⅱ）求
的长；
（Ⅲ）求二面角
的余弦值.
粤公网安备 44130202000953号