某校高二（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题．
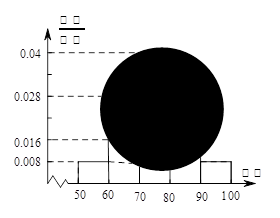
（1）求全班人数，并求出分数在
之间的频数；
（2）估计该班的平均分数，并计算频率分布直方图中间的矩形的高．
相关试题
的首项
．
对任意实数x都满足
，且
．令
.
，证明：对任意
，恒有
．
，数列
满足条件：
．
为等比数列；
令
是数
列
的前
项和，求使
成立的最
小的
.
的单调区间；
恒成立，求实数a的取值范围．
13分)设等差数列
满足
.推荐套卷
某校高二（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题．
（1）求全班人数，并求出分数在之间的频数；
（2）估计该班的平均分数，并计算频率分布直方图中间的矩形的高．
粤公网安备 44130202000953号