|
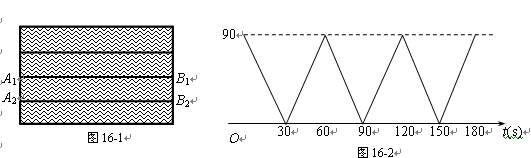
如图16-1,在一次航海模型船训练中,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲船在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙船在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两船同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲船运动时,y(m)与t(s)的函数图象如图16-2所示.
相关知识点
推荐套卷
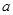 ,
,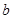 )的横纵坐标满足条件:
)的横纵坐标满足条件: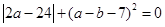 .
.
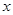 轴于A,BC⊥
轴于A,BC⊥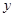 轴于C,P为CB延长线上一点,OP交BA于E,若
轴于C,P为CB延长线上一点,OP交BA于E,若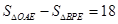 ,求P、E两点坐标。
,求P、E两点坐标。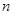 (0<
(0<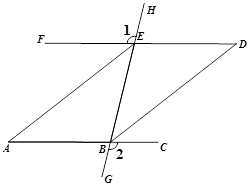
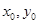 )经平移后对应点为P′(
)经平移后对应点为P′( )。
)。
 ,甲同学正确解得
,甲同学正确解得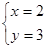 ,而乙同学粗心,把
,而乙同学粗心,把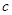 给看错了,解得
给看错了,解得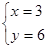 ,求
,求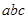 的值。
的值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号