△ABC在平面直角坐标系中的位置如图所示: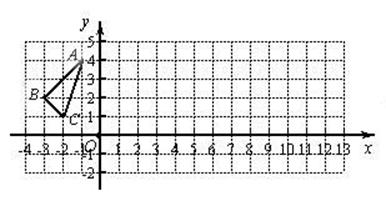
①作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
②将△ABC向右平移8个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
③观察△A1B1C1与△A2B2C2它们是否关于某直成对称?若是,请在图上画出这条对称轴.
相关知识点
推荐套卷
△ABC在平面直角坐标系中的位置如图所示:
①作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
②将△ABC向右平移8个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
③观察△A1B1C1与△A2B2C2它们是否关于某直成对称?若是,请在图上画出这条对称轴.