(本小题满分12分)在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
推荐套卷
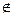 E,(3,2)
E,(3,2) (本题10分)
(本题10分)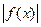 <6的解集为
<6的解集为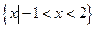 ,试求不等式
,试求不等式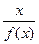 ≤1的解集.
≤1的解集. (a x+a -x), (a>0且a≠1)
(a x+a -x), (a>0且a≠1)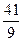 ), 求f(x)
), 求f(x) 的定义
的定义 域为集合A,
域为集合A,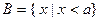
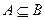 ,求a的取值范围;
,求a的取值范围;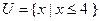 ,a=
,a=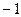 ,求
,求 .
.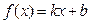 ,且
,且 ,
,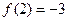 .
. 解析式
解析式 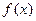 的单调性,并给予证明
的单调性,并给予证明 粤公网安备 44130202000953号
粤公网安备 44130202000953号