阅读并回答问题:
小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程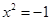 时,突发
时,突发
奇想: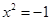 在实数范围内无解,如果存在一个数i,使
在实数范围内无解,如果存在一个数i,使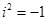 ,那么当
,那么当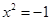 时,有
时,有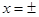 i,从而
i,从而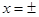 i是方程
i是方程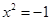 的两个根.
的两个根.
据此可知: i可以运算,例如:i3=i2·i=-1×i=-i,则i4= ,
i2011=______________,i2012=__________________;方程
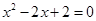 的两根为 (根用i表示).
的两根为 (根用i表示).
相关知识点
推荐套卷





 粤公网安备 44130202000953号
粤公网安备 44130202000953号