如图，直线AC∥BD，连结AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连结PA、PB，构成∠PAC、∠APB、∠PBD三个角． (提示：有公共端点的两条重合的射线所组成的角是0°)当动点P落在第①部分时，有∠APB＝∠PAC＋∠PBD，请说明理由；
当动点P落在第②部分时，∠APB＝∠PAC＋∠PBD是否成立（直接回答成立或不成立）？
当动点P在第③部分时，探究∠PAC、∠APB、∠PBD之间的关系，直接写出你发现的结论．
相关试题
(12分)如图，△ABC中,∠C=Rt∠，AB=5cm
，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1㎝，设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长。
(2)问t为何值时，
△BCP是以BC为腰的等腰三角形？
(3)另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2㎝，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动。当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
，
于
，
平分
，且
于
，与
相交于点
是
边的中点，连结
与
．
； （2）求证：
；
，
,
之间的数量关系，
班会课时，老师组织甲、乙两班同学进行投篮比赛，每班各抽5名男生和5名女生进行投篮，每人各投5次（女生投篮处距离篮筐比男生近），成绩记录如下表：
| 投进篮筐个数 |
0 |
1 |
2 |
3 |
4 |
5 |
| 甲班学生数 |
1 |
3 |
1 |
2 |
1 |
2 |
| 乙班学生数 |
0 |
1 |
2 |
4 |
2 |
1 |
根据以上提供的信息回答下列问题
（1）甲、乙两班的投篮平均成绩哪个更好？（2）甲、乙两班的投篮成绩哪个稳定？
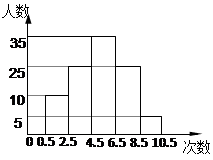
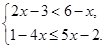
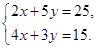
粤公网安备 44130202000953号