如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折叠边AD,使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m,0），其中m＞0.求点E、F的坐标（用含m的式子表示）；
连接OA，若△OAF是等腰三角形，求m的值；
如图（2），设抛物线y=a(x－m－6)2+h经过A、E两点，其顶点为M，连接AM，
若∠OAM=90°，求a、h、m的值.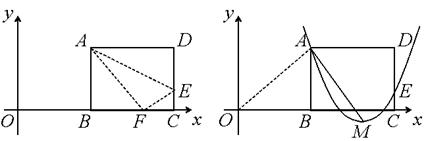 
（1） （2）
随着经济的发展，尹进所在的公司每年
都在元月一次性的提高员工当年的月工资。尹进2008年的月工资为2000元，在2010年时他的月工资增加到2420元，他2011年的月工资按2008到2010年的月工资的平均增长率继续增长．
（
1）尹进2011年的月工资为多少?
（2）尹进看了甲、乙两种
工具书的单价，认为用自己2011年6月份的月工资刚
好购买若干本甲种工具书和一些乙种工具书，当他拿着选定的这些工具书去付书款时，发现自己计算书款时把这两种工具书的单价弄对换了，故实际付款比2011年6月份的月工资少了242元，于是他用这242元又购买了甲、乙两种工具书各一本，并把购买的这两种工具书全部捐献给西部山区的学校．请问，尹进总共捐献了多少本工具书？
如图，D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF，E为垂足，EF与AB的延长线相交于点F，点O在AD上，AO＝CO，BC∥EF．
(1)证明：AB＝AC；
(2)证明：点O是△ABC的外接圆的圆心；
(3)当AB＝5，BC＝6时，连接BE，若∠ABE＝90°，求AE的长．
如图，某商标
是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
（1）求这个镶嵌图案中一个正三角形的面积；
（2）如果在这个镶嵌图案中随机确定一个点O，那么点O落在镶嵌图案中的正方形区域的概率为多少？(结果保留二位小数）
某市实施“限塑令”后，2008年大约减少塑料
消耗约4万吨．调查结
果分析显示，从2008年开始，五年内该
市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间x(年)逐年成直线上升，y与x之间的关系
如图所示
（1）求y与x之间的关系式；
（2）请你估计，该市2011年因实施“限塑令”而减少的塑料消耗量为多少？
粤公网安备 44130202000953号