探究与思考：（①题每空1分，②题每空2分，共12分）
①现定义某种运算“*”，对任意两个有理数a、b，有a*b=ab，如(-3)*2=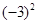
=9.
试计算： （ -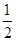
）*2 = ， (-1)*（2*3）= .
②现有若干个数，第1个数记为
，第二个数记为
，第三个数记为
……，第n个数记为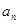
，若
，从第二个数起，每个数都等于“1与它前面的那个数的差的倒数。”
（1）试计算
（2）根据以上结果，请你写出
，
相关知识点
推荐套卷
探究与思考：（①题每空1分，②题每空2分，共12分）
①现定义某种运算“*”，对任意两个有理数a、b，有a*b=ab，如(-3)*2=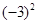=9.
试计算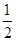： （ -）*2 = ， (-1)*（2*3）= .
②现有若干个数，第1个数记为，第二个数记为，第三个数记为……，第n个数记为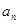，若，从第二个数起，每个数都等于“1与它前面的那个数的差的倒数。”
（1）试计算
（2）根据以上结果，请你写出，
粤公网安备 44130202000953号