已知:如图,在△ABC中, D是BC上一点,E是AD上一点,且EB=EC,∠ABE=∠ACE.
求证:∠BAE=∠CAE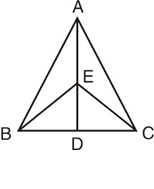
证明:在△AEB和△AEC中
∵EB=EC( )
∠ABE=∠ACE( )
AE=AE( )
∴△AEB≌△AEC( )
∴∠BAE=∠CAE( )
上面的证明过程是否正确?若认为正确,请在各步后面的括号内填入依据;若认为不正确,重新证明。.
相关知识点
推荐套卷
已知:如图,在△ABC中, D是BC上一点,E是AD上一点,且EB=EC,∠ABE=∠ACE.
求证:∠BAE=∠CAE
证明:在△AEB和△AEC中
∵EB=EC( )
∠ABE=∠ACE( )
AE=AE( )
∴△AEB≌△AEC( )
∴∠BAE=∠CAE( )
上面的证明过程是否正确?若认为正确,请在各步后面的括号内填入依据;若认为不正确,重新证明。.