已知椭圆
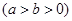的离心率为
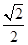，以原点为圆心，椭圆的短半轴长为半径的圆与直线
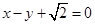相切．
（I）求椭圆
的方程；
（II）若过点
（2，0）的直线与椭圆相交于两点
，设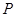
为椭圆上一点，且满足
（O为坐标原点），当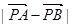
＜
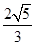时，求实数
的取值范围．
平面
，
平面
，△
，
为
的中点.
平面
；
平面
；
和平面
的侧棱长为
，
，
，
分别是
，
上的点，求
周长的最小值．
个图形的指定三视图（之一）．
推荐套卷
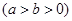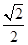已知椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线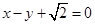相切．
（I）求椭圆的方程；
（II）若过点（2，0）的直线与椭圆相交于两点，设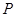为椭圆上一点，且满足（O为坐标原点），当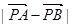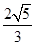＜ 时，求实数的取值范围．
粤公网安备 44130202000953号