如右图,简单组合体ABCDPE,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)若N为线段PB的中点,求证:EN⊥平面PDB;
(2)若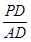 =
=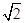 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.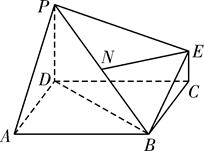
相关知识点
推荐套卷
如右图,简单组合体ABCDPE,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)若N为线段PB的中点,求证:EN⊥平面PDB;
(2)若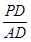 =
=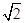 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.