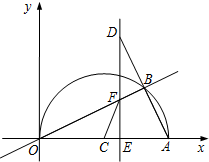
如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连接CF．当∠AOB=30°时，求弧AB的长度；
当DE=8时，求线段EF的长；
在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由．
如图1为搭建在地面上的遮阳棚，图2、图3是遮阳棚支架的示意图．遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块 ， 可分别沿等长的立柱 ， 上下移动， ．
（1）若移动滑块使 ，求 的度数和棚宽 的长．
（2）当 由 变为 时，问棚宽 是增加还是减少？增加或减少了多少？
（结果精确到 ，参考数据： ， ， ，
我国传统的计重工具 秤的应用，方便了人们的生活．如图1，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为 （厘米）时，秤钩所挂物重为 （斤 ，则 是 的一次函数．下表中为若干次称重时所记录的一些数据．
（厘米） |
1 |
2 |
4 |
7 |
11 |
12 |
（斤 |
0.75 |
1.00 |
1.50 |
2.75 |
3.25 |
3.50 |
（1）在上表 ， 的数据中，发现有一对数据记录错误．在图2中，通过描点的方法，观察判断哪一对是错误的？
（2）根据（1）的发现，问秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是多少？
一只羽毛球的重量合格标准是5.0克 克（含5.0克，不含5.2克），某厂对4月份生产的羽毛球重量进行抽样检验，并将所得数据绘制成如图统计图表．
4月份生产的羽毛球重量统计表
组别 |
重量 （克 |
数量（只 |
|
|
|
|
|
400 |
|
|
550 |
|
|
30 |
（1）求表中 的值及图中 组扇形的圆心角的度数．
（2）问这些抽样检验的羽毛球中，合格率是多少？如果购得4月份生产的羽毛球10筒（每筒12只），估计所购得的羽毛球中，非合格品的羽毛球有多少只？
粤公网安备 44130202000953号