[浙江]2012届浙江衢州地区中考试第二次模拟考试数学试卷
一个不透明的袋中装有除颜色外其余均相同的5个红球和3个黄球,从中随机摸出一个,则摸到红球的概率是( ▲ )
A.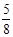 |
B.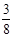 |
C.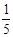 |
D.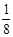 |
某工程队在金义大都市铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设 米,根据题意可列方程为( ▲ )
米,根据题意可列方程为( ▲ )
A. |
B. |
C. |
D. |
如图:等腰直角△ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线 (k≠0)与
(k≠0)与 有交点,则k的取值范围是( ▲ )
有交点,则k的取值范围是( ▲ )
A. B.
B.
C. D.
D.
北京奥运会国家体育场“鸟巢”的建筑面积为258000平方米,那么258000用科学记数法可表示为 ▲ .
如图,平面直角坐标系中,直线  与直线
与直线 交与点P,点A是直线
交与点P,点A是直线 与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
(1)当旋转角度为15°时,点P坐标为 ▲ ;
(2)整个旋转过程中,点P所经过的路线长为 ▲ .
如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米, 两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.求坡屋顶高度CD的长度;
求斜面钢条AC的长度.(长度精确到0.1米)

下面图①,图②是某校随机调查部分学生是否知道母亲生日情况的扇形统计图和条形统计图:
根据上图信息,解答下列问题求本次被调查学生的人数,并补全条形统计图
若全校共有1620名学生,你估计这所学校有多少名学生知道母亲的生日?
通过对以上数据的分析,你有何感想?(用一句话回答)
某中学九年级甲、乙两班同学商定举行一次远足活动,A、B两地相离10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地,两班同学各自到达目的地后都就地活动. 两班同时出发,相向而行. 设步行时间为x小时,甲、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题:
分别求出y1、y2与x的函数关系式
求甲、乙两班学生出发后,几小时相遇?
如图,在正方形ABCD中, E是AB上一点,F是AD延长线上一点,且
DF=BE= BC=1.
BC=1.
求证:CE=CF;
若G在AD上,连结GC,且∠GCE=45°,求∠GCF的度数
在(2)的条件下,求GC的长度.
如图1,点C、B分别为抛物线C1:y1=x2+1,抛物线C2:y2=a2x2+b2x+c2的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB=BD.求点A的坐标:
如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”.其他条件不变,求CD的长和a2的值;
如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 2
 (直接写结果).
(直接写结果).
 的绝对值是( ▲ )
的绝对值是( ▲ )

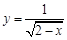 中,自变量
中,自变量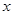 的取值范围是( ▲ )
的取值范围是( ▲ )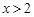
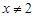
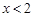
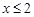
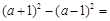 ( ▲)
( ▲)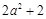
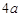
 的解集在数轴上表示正确的是 ( ▲ )
的解集在数轴上表示正确的是 ( ▲ )

 = ▲ .
= ▲ . 的解是 ▲ .
的解是 ▲ . .
. ,其中
,其中 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号