山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
相关知识点
推荐套卷
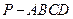

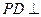
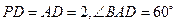 ,
,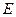 、
、 分别为
分别为 、
、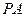 的中点。
的中点。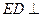 平面
平面 ;
; 的体积;
的体积;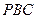 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。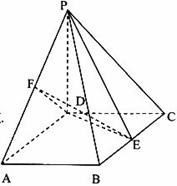



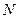
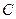

 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;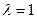 时,
时,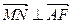 ;
;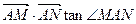 =6
=6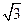 时, 求直线MN的方程
时, 求直线MN的方程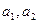 的值;
的值;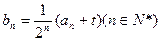 ,是否存在一个实数
,是否存在一个实数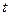 ,使数列
,使数列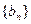 为等差数列?若存在,求出实数
为等差数列?若存在,求出实数 }的前n项和
}的前n项和

 在区间
在区间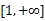 内单调递增,求a的取值范围
内单调递增,求a的取值范围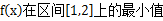
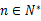 ,且
,且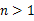 时,都有
时,都有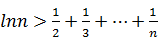
 的最小正周期;
的最小正周期;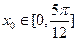 ,使不等式
,使不等式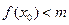 成立,求函数
成立,求函数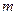 的取值范围
的取值范围 粤公网安备 44130202000953号
粤公网安备 44130202000953号