某市第一中学要用鲜花布置花圃中
五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择．
（1）当
区域同时用红色鲜花时，求布置花圃的不同方法的种数；
（2）求恰有两个区域用红色鲜花的概率；
（3）记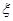
为花圃中用红色鲜花布置的区域的个数，求随机变量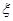的分布列及其数学期望.
相关试题
，其中a≥b>c,a+b+c=0.
有两个零点；
上的最小值为1，最大值为13，求a、b、c的值.
.
；
,AB=1.
中，
.求
,c="2" ,b=3.相关知识点
推荐套卷
某市第一中学要用鲜花布置花圃中五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择．
（1）当区域同时用红色鲜花时，求布置花圃的不同方法的种数；
（2）求恰有两个区域用红色鲜花的概率；
（3）记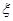为花圃中用红色鲜花布置的区域的个数，求随机变量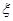的分布列及其数学期望.
粤公网安备 44130202000953号