已知极点与坐标原点O重合，极轴与x轴非负半轴重合，M是曲线C: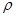 
=4sin
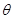上任一点，点P满足
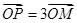．设点P的轨迹为曲线Q．
（1）求曲线Q的方程；
（2）设曲线Q与直线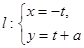
（t为参数）相交于A、B两点，且|AB|=4．求实数a．
相关试题
的前
项和为
，且满足
，
。
与
的关系式，并求
。
的内角
所对的边分别为
，且
。
，求
的值； （Ⅱ）若
，求
的值。
。
的最小值；（2）解不等式
。
过点
，且倾斜角为
，圆方程为
。
的值。
上是减函数，且
.
Ⅰ）求
的值，并求出
和
的取值范围;
；
求
的取值范围，并写出当
的解析式.推荐套卷
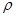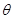已知极点与坐标原点O重合，极轴与x轴非负半轴重合，M是曲线C: =4sin上任一点，点P满足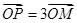．设点P的轨迹为曲线Q．
（1）求曲线Q的方程；
（2）设曲线Q与直线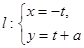（t为参数）相交于A、B两点，且|AB|=4．求实数a．
粤公网安备 44130202000953号