19． (本小题满分12分)
如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠DAB = 60°的菱形，AC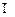
BD = O，A1C1
B1D1 = O1，E是O1A的中点．
(1) 求二面角O1－BC－D的大小；
(2) 求点E到平面O1BC的距离．
|
相关试题
满足
，其中
且
．
时，
，求实数
的取值集合；
时，
恒成立，求
的取值范围．
的极坐标方程为
，
分别为
轴、
轴的交点，曲线
的参数方程为
（
为参数，且
），
为
（
为坐标原点）的直线与曲线
形的面积。
是函数
图
象的一条对称轴，对于任意
， 
, 当
≤
≤
时，
.
时，求：函数
，命题
（
），且
是
的必要不充分条件，求实数
的取值范围。
中，
，
．
的值；（Ⅱ）设
，求推荐套卷
19． (本小题满分12分)
如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠DAB = 60°的菱形，AC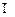BD = O，A1C1B1D1 = O1，E是O1A的中点．
(1) 求二面角O1－BC－D的大小；
(2) 求点E到平面O1BC的距离．
|
粤公网安备 44130202000953号