任何一个正整数n都可以进行这样的分解：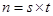
（s、t是正整数，且s≤t），如果
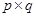在n的所有这种分解中两因数之差的绝对值最小，我们就称（
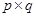）是n的最佳分解，并规定
．例如：18可以分解成1×18，2×9，3×6，这时就有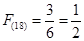
．结合以上信息，给出下列关于
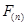的说法：①
；②
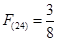；③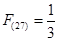
；④若n是一个整数的平方，则
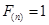．其中正确的说法有_________.（只填序号）
。
，若
， 
，则
，则
________
=，
=.
时，
有意义。
相关知识点
推荐套卷
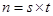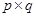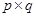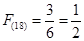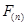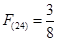任何一个正整数n都可以进行这样的分解： （s、t是正整数，且s≤t），如果在n的所有这种分解中两因数之差的绝对值最小，我们就称（）是n的最佳分解，并规定．例如：18可以分解成1×18，2×9，3×6，这时就有．结合以上信息，给出下列关于的说法：①；②；③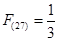；④若n是一个整数的平方，则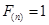．其中正确的说法有_________.（只填序号）
粤公网安备 44130202000953号