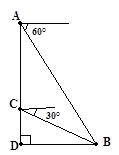青青草原上，灰太狼每天都想着如何抓羊，而且是屡败屡试，永不言弃.（如图所示）一天，灰太狼在自家城堡顶部A处测得懒羊羊睡觉所在地B处的俯角为60°，然后下到城堡的C处，测得B处的俯角为30°.已知AC=40米，若灰太狼以5m/s的速度从城堡底部D处出发，几秒钟后能抓到懒羊羊？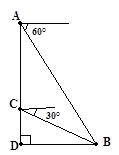
，
，
，求
的值.
， （2）
与
是同类项.求代数式：
的值.
的2倍得
，求这个多项式
，其中
，
。
相关知识点
推荐套卷
青青草原上，灰太狼每天都想着如何抓羊，而且是屡败屡试，永不言弃.（如图所示）一天，灰太狼在自家城堡顶部A处测得懒羊羊睡觉所在地B处的俯角为60°，然后下到城堡的C处，测得B处的俯角为30°.已知AC=40米，若灰太狼以5m/s的速度从城堡底部D处出发，几秒钟后能抓到懒羊羊？
粤公网安备 44130202000953号